This module implements the Lennard-Jones potential with a linear truncation scheme (which is equivalent to a shifted force),
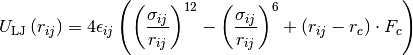
for the interaction between two particles of species 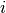 and
and
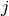 . Here,
. Here, 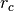 denotes the cutoff distance and
denotes the cutoff distance and 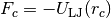 the force at the cutoff for the untruncated potential.
the force at the cutoff for the untruncated potential.
This linear truncation scheme modifies the potential drastically and at all distances by adding a constant force, and we do not recommend it for future work. It is mainly provided for historical reasons to connect to existing data and publications. Please refer to the local r⁴ truncation scheme for an alternative.
Construct linearly truncated Lennard-Jones potential.
| Parameters: |
|
|---|
If all elements of a matrix are equal, a scalar value should be passed instead.
Note
The cutoff is only relevant with halmd.mdsim.forces.pair_trunc.
Matrix with elements 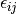 .
.
Matrix with elements 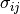 .
.
Matrix with elements 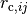 in reduced units.
in reduced units.
Matrix with elements 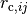 in units of
in units of 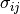 .
.
Name of potential for profiler.