Potential truncations¶
sharp¶
Create sharp truncation by setting the potential to zero for particle
distances  larger than the cutoff distance
larger than the cutoff distance 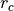 , i.e., by multiplying
with a step function:
, i.e., by multiplying
with a step function:
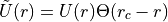
Both potential and force are discontinuous at the cutoff.
Example:
potential = potential:truncate({"sharp", cutoff = 4})
shifted¶
Amend the sharp truncation by an energy shift such that the potential is
continuous at the cutoff distance 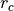 :
:
![\tilde U(r) = [U(r) - U(r_c)] \Theta(r_c - r)](../../../../../_images/math/370fddb0d36a10d9f14278b37e9e9011083ad060.png)
The force is not affected by this and remains discontinuous at the cutoff.
Example:
potential = potential:truncate({"shifted", cutoff = 2.5})
force_shifted¶
Amend the energy-shifted potential by a linear term, effectively shifting
the force to zero at the cutoff distance 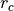 :
:
![\tilde U(r) = [U(r) - U(r_c) - (r - r_c) U'(r_c)] \Theta(r_c - r)](../../../../../_images/math/49fd1c69c6f407c176655ab9ea56879d1d687c27.png)
Both energy and force are continuous at the cutoff. Note that this modification globally tilts the potential with possible physical implications for, e.g., phase diagrams.
Example:
potential = potential:truncate({"force_shifted", cutoff = 2.5})
smooth_r4¶
Truncate the potential  such that it remains a C²-continuous
function at the cutoff, i.e., the force being continuously differentiable.
As a consequence, momentum and energy drift are drastically diminished
even from long runs using symplectic integrators such as
such that it remains a C²-continuous
function at the cutoff, i.e., the force being continuously differentiable.
As a consequence, momentum and energy drift are drastically diminished
even from long runs using symplectic integrators such as
halmd.mdsim.integrators.verlet.
The truncation is implemented by multiplication of the energy-shifted potential with the local smoothing function
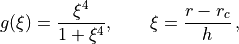
where 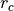 is the cutoff distance, and the parameter
is the cutoff distance, and the parameter
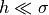 , which has the dimension of a length, controls the the
range of smoothing. The C²-continuous truncated potential then reads
, which has the dimension of a length, controls the the
range of smoothing. The C²-continuous truncated potential then reads
![\tilde U(r) = [U(r) - U(r_c)] \, g\left(\frac{r - r_c}{h}\right) \Theta(r_c - r),](../../../../../_images/math/10ad300ce929e5be1283754d043cc87a74318a98.png)
and the C¹-continuous force is
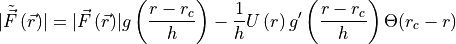
with the derivative of the smoothing function
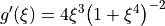 .
.
Example:
potential = potential:truncate({"smooth_r4", cutoff = 2.5, h = 0.005})
The following figure shows unmodified and C²-smooth variants of the
Weeks-Chandler-Andersen potential, the repulsive part of the Lennard-Jones
potential sharply cutoff at ![r_c = \sqrt[6]{2}](../../../../../_images/math/a6f1a7612bed1bb1ffa49c95bc933823780579e4.png) .
.
(Source code, png, hires.png, pdf)
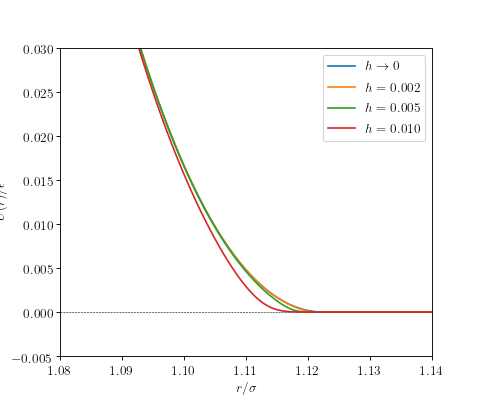
The following figure shows the absolute value of the force.
(Source code, png, hires.png, pdf)

