Thermodynamics¶

This module calculates the instantaneous values of thermodynamic state variables for the particles of a given group.

class halmd.observables.thermodynamics(args)¶

Construct thermodynamics module.

Parameters:	args (table) – keyword arguments args.group – instance of `halmd.mdsim.particle_groups` args.force – instance of `halmd.mdsim.forces` args.box – instance of `halmd.mdsim.box`

nparticle()¶: Returns the number of particles 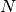$N$ selected by args.group.

density()¶: Returns the number density $\rho = N / V$ using the volume from args.box.

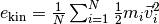kinetic_energy()¶: Returns the mean kinetic energy per particle: $e_{\text{kin}} = \frac{1}{N} \sum_{i=1}^N \frac{1}{2} m_i \vec v_i^2$ .

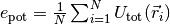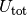potential_energy()¶: Returns the mean potential energy per particle: $e_{\text{pot}} = \frac{1}{N} \sum_{i=1}^N U_{\text{tot}}(\vec r_i)$ , where $U_{\text{tot}}$ denotes the sum of external and pair potentials.

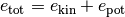total_energy()¶: Returns the mean total energy per particle: $e_{\text{tot}} = e_{\text{kin}} + e_{\text{pot}}$ .

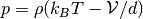pressure()¶: Returns the pressure computed from the virial: $p = \rho (k_B T - \mathcal{V} / d)$ .

temperature()¶: Returns the instantaneous temperature as given by the kinetic energy: $k_B T = 2 e_{\text{kin}} / d$ .

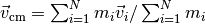center_of_mass_velocity()¶: Returns the centre-of-mass velocity: $\vec v_{\text{cm}} = \sum_{i=1}^N m_i \vec v_i / \sum_{i=1}^N m_i$ .

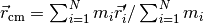center_of_mass()¶: Returns the centre of mass: $\vec r_{\text{cm}} = \sum_{i=1}^N m_i \vec r_i' / \sum_{i=1}^N m_i$ , where $\vec r_i'$ refers to absolute particle positions, i.e., extended by their image vectors for periodic boundary conditions.

mean_mass()¶: Returns the mean particle mass: $\bar m = \frac{1}{N} \sum_{i=1}^N m_i$ .

virial()¶: Returns mean virial per particle as computed from the trace of the potential part of the stress tensor:

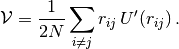
$\mathcal{V} = \frac{1}{2 N} \sum_{i \neq j} r_{ij} \, U'(r_{ij}) \, .$

hypervirial()¶

Returns the mean hypervirial per particle, see the book by M. P. Allen and D. J. Tildesley (Clarendon Press, Oxford, 1987) for a definition. This quantity may be used to determine the isochoric compressibility from NVE simulations, which does not work very well in practice. A superior route is to extrapolate the static structure factor to zero wavenumber.

This method will be deprecated in the next release.

stress_tensor()¶

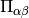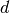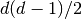Returns the elements of the stress tensor $\Pi_{\alpha\beta}$ as a vector. The first $d$ (= dimension) elements contain the diagonal followed by $d(d-1)/2$ off-diagonal elements 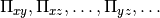$\Pi_{xy}, \Pi_{xz}, \dots, \Pi_{yz}, \dots$ The stress tensor is computed as

$\Pi_{\alpha\beta} = \sum_{i=1}^N \left[ m_i v_{i\alpha} v_{i\beta} + \frac{1}{2}\sum_{j \neq i} \frac{r_{ij\alpha} r_{ij\beta}}{r_{ij}} \, U'(r_{ij}) \right] \/,$

where $\vec r_{ij} = \vec r_i - \vec r_j$ in nearest image convention.

dimension¶: Space dimension 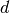$d$ of the simulation box as a number.

group¶: Instance of halmd.mdsim.particle_groups used to construct the module.

writer(args)¶

Write state variables to a file.

Parameters:	args (table) – keyword arguments args.file – instance of file writer args.every (number) – sampling interval args.location (string table) – location within file (optional) args.fields (table) – data fields to be written (optional)
Returns:	instance of group writer

The argument location specifies a path in a structured file format like H5MD given as a table of strings. If omitted it defaults to {"observables", group.label}.

The table fields specifies which data fields are written. It may either be passed as an indexed table, e.g. {"pressure"}, or as a dictionary, e.g., {p = "pressure"}; the table form is interpreted as {pressure = "pressure", …}. The keys denote the field names in the file and are appended to location. The values specify the data methods of the thermodynamics module, i.e., all methods described above except for dimension and group. The default is {"potential_energy", "pressure", "temperature", "center_of_mass_velocity"}.

disconnect()¶: Disconnect thermodynamics writer from observables sampler.

Navigation

Quick search

Thermodynamics¶

Navigation