Helfand Moment

This module calculates mean-square difference of the Helfand moment for the stress tensor [1][2],

\delta G^2_{\alpha\beta}(t) := \frac{1}{N} \bigl\langle [G_{\alpha\beta}(t) - G_{\alpha\beta}(0)]^2 \bigr\rangle \qquad \alpha, \beta \in \{x, y, z\} \, ,

where the Helfand moment G_{\alpha\beta}(t) is defined as the time integral of the stress tensor \Pi_{\alpha\beta}(t),

G_{\alpha\beta}(t) = \int_0^t \! \Pi_{\alpha\beta}(t') \, \mathrm{d}t' \approx \sum_{k=0}^{n-1} \Pi_{\alpha\beta}(k \delta t) \, \delta t \, \qquad t = n \, \delta t \, .

The normalisation with the particle number 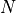N renders \delta G^2_{\alpha\beta}(t) finite in the thermodynamic limit. The stress tensor is obtained from halmd.observables.thermodynamics.stress_tensor(), and the integral is computed numerically over discrete time intervals \delta t using halmd.observables.utility.accumulator.

The shear viscosity 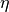\eta is obtained from \delta G^2_{\alpha\beta}(t) by virtue of the Einstein–Helfand relation

\eta = \frac{\rho}{k_B T} \lim_{t\to\infty} \frac{\mathrm{d}}{2 \mathrm{d}t} \delta G^2_{\alpha\beta}(t) \, .

[1]B. J. Alder, D. M. Gass, and T. E. Wainwright, Studies in molecular dynamics. VIII. The transport coefficients for a hard-sphere fluid, J. Chem. Phys. 53, 3813 (1970) [Link].
[2]S. Viscardy and P. Gaspard, Viscosity in molecular dynamics with periodic boundary conditions, Phys. Rev. E 68, 041204 (2003) [Link].

Note

The module returns the sum over all off-diagonal elements, \sum_{\alpha < \beta} \delta G^2_{\alpha\beta}(t) analogously to halmd.observables.dynamics.mean_square_displacement.

class halmd.observables.dynamics.helfand_moment(args)

Construct Helfand moment

This module implements a halmd.observables.dynamics.correlation module.

Parameters:
  • args – keyword arguments
  • args.thermodynamics – instance of halmd.observables.thermodynamics
  • args.interval (number) – time interval for the integration of the stress tensor in simulation steps
acquire()

Acquire stress tensor

Returns:Stress tensor sample
correlate(first, second)

Correlate two stress tensor samples.

Parameters:
  • first – first phase space sample
  • second – second phase space sample
Returns:

mean-square integral of the off-diagonal elements of the stress tensor
desc

Module description.

disconnect()

Disconnect module from core.

class writer(args)

Construct file writer.

Parameters:
  • args (table) – keyword arguments
  • args.file – instance of file writer
  • args.location (string table) – location within file (optional)
Returns:

file writer as returned by file:writer().

The argument location specifies a path in a structured file format like H5MD given as a table of strings. It defaults to {"dynamics", self.label, "mean_square_helfand_moment"}.